Joint Depth-Texture Bit Allocation

In this chapter, we propose a novel joint depth-texture bit-allocation algorithm for the joint compression of texture and depth images. The described algorithm combines the depth and texture Rate-Distortion (R-D) curves to obtain a single R-D surface that allows the optimization of the joint bit-allocation problem in relation to the obtained rendering quality. We subsequently discuss a fast hierarchical optimization algorithm that exploits the smooth monotonic properties of the R-D surface. The hierarchical optimization algorithm employs an orthogonal search pattern, so that the number of image-compression iterations for measuring quality is minimized. Experimental results show an estimated gain of 1 dB compared to a compression performed without joint bit-allocation optimization. Besides this advantage, our joint model can be readily integrated into an N-depth/N-texture multi-view encoder, as it yields the optimal compression setting with a limited computation effort.

Introduction

In Chapter 4, we have seen that a possible 3D video representation format relies on a technique that associates one depth with one texture image. To enable the 3D-TV application, a simplifed version of this representation format, i.e., the 1-depth/1-texture format, was recently adopted and standardized in Part 3 of the MPEG-C video specifications [76]. Following this initiative, a more advanced N-depth/N-texture format is currently investigated by the Ad Hoc Group on Free Viewpoint Television (FTV) [77]. The FTV framework is based on a representation that combines a reference texture image with the corresponding depth image that describes the depth of the visible surfaces in the scene. Using a depth-image-based representation, the 3D rendering of novel views can be subsequently performed, using image warping algorithms. Thus, employing a depth-image-based representation in transmission leads to the compression of multiple texture views and also their associated depth images.

Previous work on the compression of such a data set (texture and corresponding depth images), has addressed the problem of texture and depth compression by coding each of the signals individually. For example, several approaches have employed a modified H.264/MPEG-4 AVC encoder to compress either texture [78], or depth [20], [23] data. Such an independent coding yields high compression ratios for texture and depth data, individually. However, the influence of texture and depth compression on 3D rendering is not incorporated in these experiments, so that the rendering quality trade-off are not considered. Furthermore, recent literature [54], [79] confirms that the rendering quality trade-off is sometimes not well understood.

To illustrate the problem of joint compression of texture and depth, let us consider the following two cases. First, assume that the texture and depth images are compressed at very high and low quality, respectively. In this case, detailed texture is mapped onto a coarse approximation of object surfaces, which thus yields rendering artifacts. Alternatively, when texture and depth images are compressed at low and high quality, respectively, a high-quality depth image is employed to warp a coarsely quantized texture image, which also yields low-quality rendering. These two simple but extreme cases illustrate that a clear dependence exists between the texture- and depth-quality setting. It goes without saying that this dependency exists in the general case as well. Consequently, the quantization setting for both the depth and texture images should be carefully selected. For this reason, we address in this chapter, the following problem statement:
given a maximum bit-rate budget to represent the 3D scene, what is the optimal distribution of the bit rate over the texture and the depth image, such that the 3D rendering distortion is minimized?

To answer this question, we propose a new compression algorithm with a bit-rate control that unifies the texture and depth Rate-Distortion (R-D) functions. The attractiveness of the algorithm is that both depth and texture data are simultaneously combined into a joint R-D surface model that calculates the optimal bit allocation between texture and depth. We discuss the optimization of the performance of the joint coding algorithm using a slightly extended H.264/MPEG-4 AVC encoder, where the extension involves a joint bit-allocation algorithm. However, note that the proposed extension can be employed as an addition to any encoder, e.g., H.264/MPEG-4 AVC, JPEG-2000 or even a platelet-based encoder. Additionally, we have found that our joint model can be readily integrated as a practical sub-system, because it influences the setting of the compression system rather than the actual coding algorithm. As a bonus, this optimal setting is obtained with a limited computation effort.

The remainder of this chapter is structured as follows. Section 7.2 formulates the framework of the joint bit allocation of texture and depth. Section 7.3 describes a fast hierarchical optimization algorithm. Section 7.4 discusses the relationship between the depth and texture bit rate and Section 7.5 presents the possible applications of the proposed algorithm. Experimental results are provided in Section 7.6 and the chapter concludes with Section 7.7.

Joint depth/texture bit allocation

In this section, we first present a joint bit-allocation analysis of depth and texture and afterwards, we provide an experimental analysis of the two-dimensional R-D model to enable a fast search algorithm for estimating the optimal quantization parameters.

Formulation of the joint bit-allocation problem

Let us consider the problem of jointly coding a texture and depth image at a maximum rate \(R_{max}\) with minimum rendering distortion \(D_{render}\). The rate \(R_{max}\) and distortion \(D_{render}\) functions can be defined as follows. First, the maximum rate value \(R_{max}\) is decomposed into the sum of the individual rates required for texture and depth coding. Because the texture and depth images are coded with two different quantizer settings (denoted \(q_t\) and \(q_d\), respectively), the texture and depth rate functions can be written as \(R_t(q_t)\) and \(R_d(q_d)\), respectively. The joint rate function can therefore be specified as \[R_{max}(q_t,q_d)=R_t(q_t) + R_d(q_d).\] Second, the rendering distortion function \(D_{render}\) depends on the image rendering algorithm. The rendering algorithm relies on the quality of the input texture and depth images and therefore on the quantization parameters \(q_t\) and \(q_d\). Consequently, as there is one rendering quality, we define a joint rendering distortion as \(D_{render}(q_t,q_d)\).

The goal of the joint bit-allocation optimization is to determine the optimal quantization parameters \((q_t^{opt},q_d^{opt})\) for coding the depth and texture images, such that the rendering distortion is minimized. The optimization problem can now be formulated as finding the minimum of the rendering distortion, hence \[(q_t^{opt},q_d^{opt})={\mathop{\textrm arg\, min}}_{q_d,q_t \in Q} D_{render}(q_t,q_d), \label{eq:OptQuantizationParameters}\] under the constraint that the joint bit rate is bounded to \(R_{max}\), so that \[R_t(q_t^{opt})+R_d(q_d^{opt}) \le R_{max},\] where \(Q\) denotes the set of all possible quantizer settings. Without prior assumption, the solution to Equation (7.2) involves an exhaustive search over \(Q\), in order to find the quantization setting with minimum distortion. Fortunately, a more efficient search can be performed by exploiting special properties of the R-D function. For example, assuming a smooth monotonic R-D surface model, hierarchical optimization techniques can be employed to find the best setting. Therefore, prior to investigating fast search algorithms, we provide a performance-point analysis of the R-D function to validate the smoothness of the surface.

R-D surface analysis

To analyse the R-D function, we construct a surface using an input data set, composed of multi-view images and their corresponding depth images. The rendering algorithm is based on the relief texture mapping (see Chapter 4). We generate the R-D surface by measuring the rendering distortion for all quantizers \((q_t,q_d)\), defined within a search range of \(q_{min} \leq q_t,q_d\leq q_{max}\). In total, \(k=q_{max}-q_{min}+1\) compression iterations of the depth and texture images are carried out, which yields \(k \times k\) R-D performance points. In our specific case, we employ an H.264/MPEG-4 AVC encoder to compress the reference texture and depth images. However, since the proposed joint bit-allocation method is generic, any depth and texture encoder can be employed, as long as they have a controllable quantizer.

To measure the rendering distortion, one solution is to warp a coded reference image using the corresponding depth image. The rendering distortion is evaluated by calculating the Mean Squared Error (MSE) between the rendered image and the corresponding image captured at the same location and orientation (see Figure 7.1).

Figure 7.1 The rendering distortion is obtained by rendering a synthetic image at the position of a neighboring camera. The rendering distortion is then evaluated by calculating the MSE between the original captured image and the rendered view.

Therefore, considering an \(N\)-view data set and a selected quantizer set \((q_t,q_d)\), \(N-r\) distortion measures can be obtained (excluding the \(r\) reference images). To obtain a single rendering distortion measurement, the \(N-r\) measures are then averaged. The pseudo-code of the R-D surface construction algorithm is summarized in Algorithm 5.

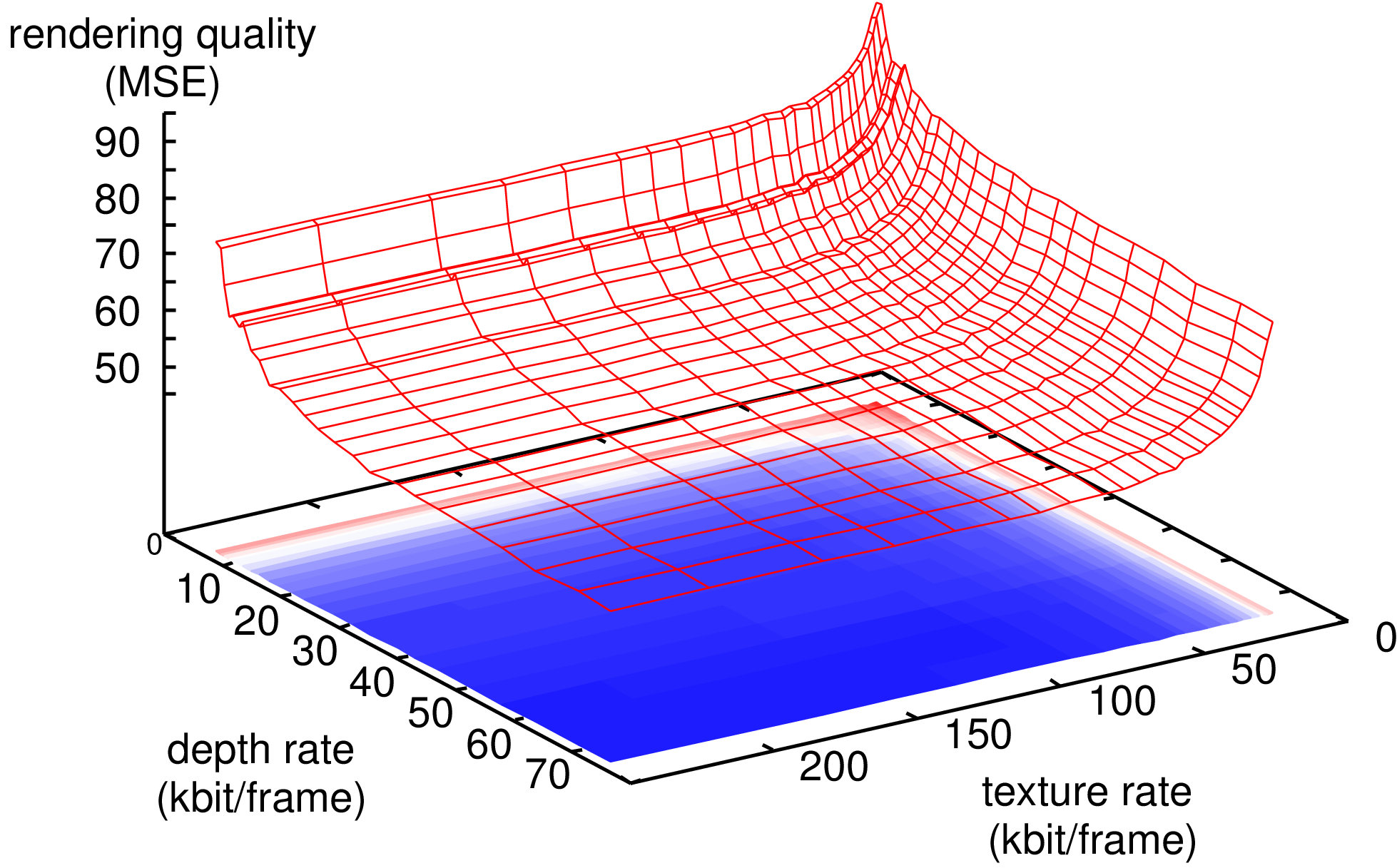
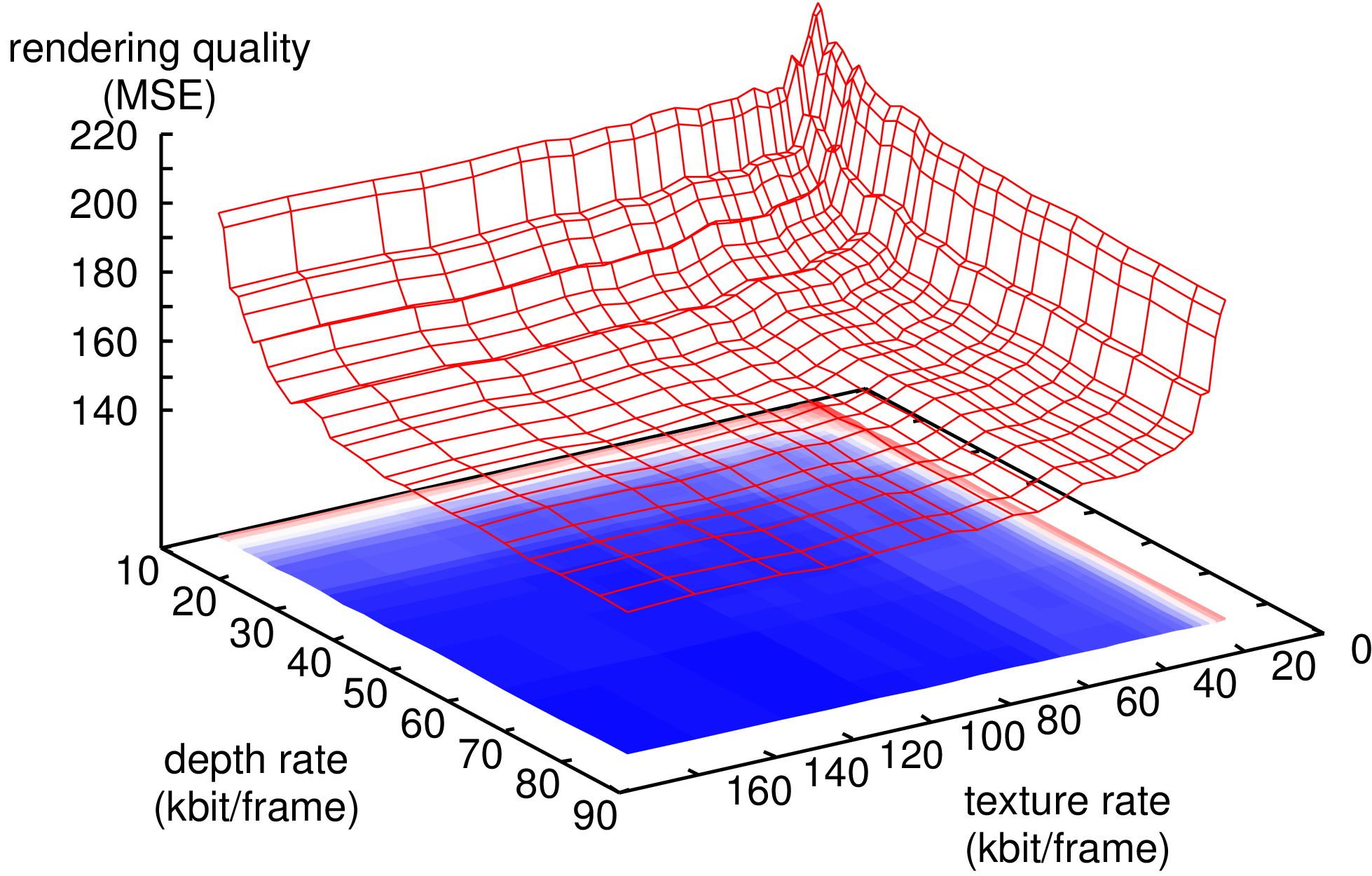
As a result, Figure 7.2 shows the R-D surfaces of the two multi-view sequences “Ballet” and “Breakdancers”. To generate the presented curves, the first depth and texture of the reference views are encoded with an H.264/MPEG-4 AVC encoder in intra-mode.

(a)

(b)

Figure 7.2 (a) R-D surface for the depth and texture of the “Breakdancers” sequence. (b) R-D surface for the depth and texture of the “Ballet” sequence. Note the difference in scale of the rendering quality.

Considering Figure 7.2, it is readily observed that both R-D surfaces show smooth monotonic properties. Up till now, we have only established an empirical validation of monotonic nature of the R-D surface. Assuming that the rendering function is indeed monotonic, a fast quantizer-setting search algorithm can be employed.

Hierarchical search optimization

The guiding principle of the hierarchical optimization is to perform a recursive, coarse-to-fine, search of the optimal quantization setting. The algorithm is summarized as follows. First, a search over a limited number of quantizer candidate settings \((q_t,q_d)\) is performed. Practically, we employ nine candidates shown as black R-D points and organized them in a search pattern, as illustrated by Figure 7.3. Second, the algorithm selects the candidate with the lowest rendering distortion that satisfies the maximum bit-rate constraint. The search range is then refined and the process is recursively performed by using the selected quantizer set as an initialization, similar to the well-known Three-Step Search in motion estimation [108]. The minimum corresponds to the lowest distortion point after the last recursion.

This technique has two advantages. First, the hierarchical set-up of the search significantly reduces the computational complexity by reducing the possible amount of quantizer candidate settings. Second, by employing an appropriate search pattern, the number of iterations for texture and depth image compression can be decreased. For example, it can be observed in Figure 7.3 that the \(3 \times 3\) orthogonal pattern of the dark R-D points enable the re-use of depth and texture images, so that only six compression iterations are required. Following this in the second step, by using the pre-defined grid, only four compression iterations of depth and texture images are necessary to obtain again nine R-D points (shown as dark grey in Figure 7.3. In contrast to this, a less-structured search such as a descent method, would require a much larger number of image-compression operation points.

The previous considerations rely considerably on the assumption that the rate-distortion surface model shows reasonable smooth monotonic behavior. This behavior is plausible because it combines two smooth monotonic R-D curves from the individual signals. This is typically achieved with properly designed coding and rendering sub-systems. Only poorly designed systems would show a less smooth, noisy behavior. Having said this, the use of a fast algorithm is even an advantage compared to a descent method because it comes faster to a similar result. The hierarchical search algorithm is summarized in Algorithm 6.

Figure 7.3 Hierarchical search pattern of the involved quantization settings.

Relationship between the depth and texture bit rate

A recurring question in literature on multi-view depth and texture coding is how the bit rate is distributed over texture and depth [54]. A common approach is to employ fixed ad-hoc quantization settings that enable a sufficient rendering quality for most multi-view sequences. Practically, it means that the depth bit rate is restricted to an arbitrarily selected percentage/ratio of the total bit rate, e.g., \(10-20\%\) of the total bit rate. However, this approach of employing a-priori fixed ad-hoc quantizer settings is not appropriate because of the two factors that influence the bit-rate ratio between the depth and texture. The first factor is the individual complexity of the depth and texture images, and thus, the corresponding bit rate required for encoding. More specifically, there exists no fixed relationship that couples the complexity of the texture and the depth signal. Our aim is to show that fixed quantizer settings are not optimal for joint encoding of the multi-view depth and texture video and that a joint optimization of the independent quantizers is preferred. The second factor that influences the rendering quality, and thus, the depth and texture bit-rate ratio, is the number of reference views employed for rendering. For example, it can be readily understood that employing a large number of reference views yields a high rendering quality. Therefore, an optimization of the quantization parameters should be performed not only for a specific multi-view sequence, but also for the selected number of reference views. Therefore, Section 7.6 presents experimental results obtained from using two different multi-view sequences while also employing one and two reference views.

Applications of the joint bit-allocation framework

From the viewpoint of the system designer, the proposed joint bit-allocation algorithm can be incorporated into various 3D video systems.

1. Visual rendering only. The first possibility is to integrate the proposed algorithm into a 3D-TV system for solely maximizing the rendering quality. The proposed algorithm can be further integrated into the 3D-TV video processing system to optimize the quantizer settings such that the visual rendering quality is maximized within the N-depth/N-texture coding framework.

2. View prediction/coding. The second possibility is to integrate the proposed algorithm into a multi-view texture encoder, as proposed in Chapter 5. Specifically, we have shown that image rendering can be used as a view-prediction algorithm and can be incorporated into an H.264/MPEG-4 AVC encoder to compress multi-view video. Because such a multi-view encoder relies on a depth image for view prediction, an appropriate depth quantizer that maximizes the prediction quality should be selected. Hence, by calculating optimal quantizer settings, the proposed algorithm maximizes the rendering quality, i.e., the view-prediction accuracy, such that a high coding performance is obtained.

Summarizing, the joint R-D algorithm attemps to maximize the rendering quality under a bit-rate constraint. This can be employed for rendering only, or for maximizing the view-prediction accuracy in the encoder, when that view prediction is applied in the coding algorithm. In both cases, no further parameter optimizations are carried out at the decoder and it will simply adopt the optimal quantizer settings for depth and texture and perform rendering accordingly.

Experimental results

To evaluate the performance of the search algorithm for the quantizer settings, experiments are carried out, using the “Ballet” and “Breakdancers” sequences. The impact of using a variable number of reference views is measured by using two different, so called, rendering structures. As portrayed by Figure 7.4 (a) and (b), the investigated rendering structures include one and two reference views, respectively.

(a)

(b)

Figure 7.4 Rendering structures based on (a) one reference view and (b) two reference views.

To generate the R-D surfaces for both sequences, we set \(q_t^{min}=q_d^{min}=27\) and \(q_t^{max}=q_d^{max}=51\), so that \(25 \times 25\) R-D points are obtained. For coding experiments, we have employed the open-source H.264/MPEG-4 AVC encoder x264 [86] and we have encoded the first depth and texture frames of the reference view(s) in intra-mode. The presented experiments attempt to quantify the rendering quality obtained in three ways by using:

• a pre-defined depth bit rate (reserve \(10\%\) of the texture bit rate), or

• the quantizers \(q_d,q_t\) determined by performing a full search, or

• the quantizers \(q_d,q_t\) determined by employing a hierarchical search.

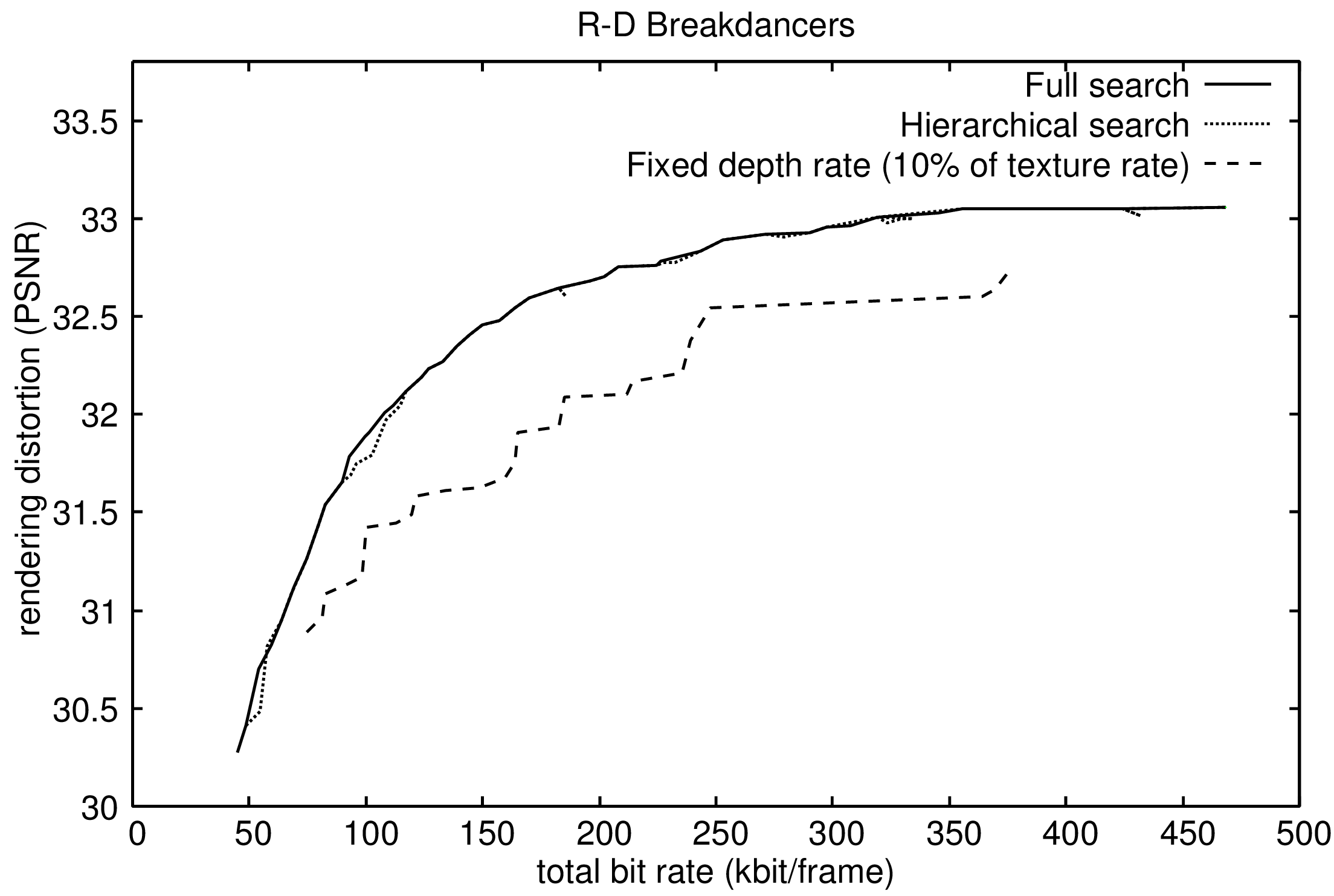
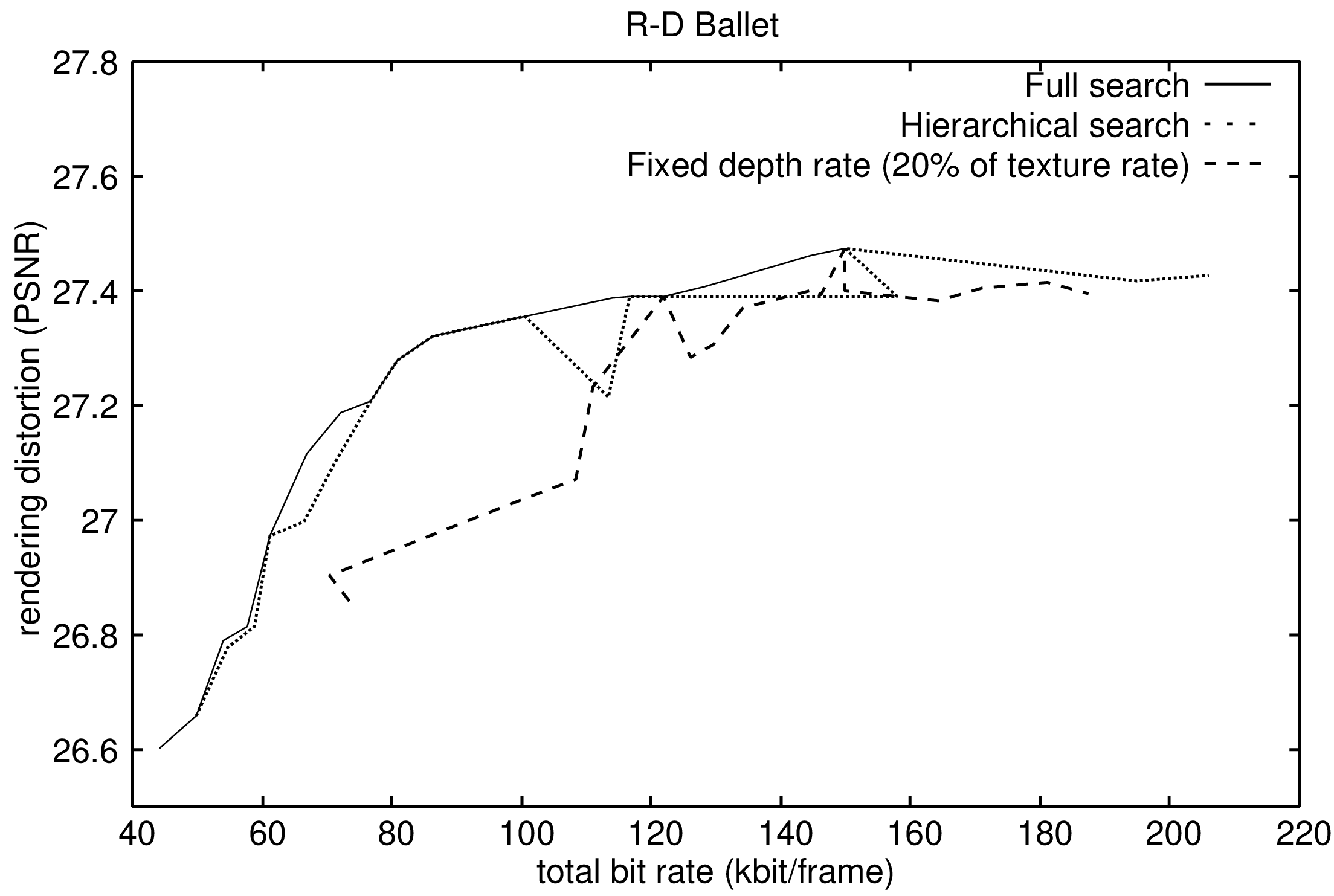
The pre-defined depth bit rate of \(10\%\) is based on experimental results published in the framework of the ATTEST project jointly carried out by Op De Beeck et al. and Smolic et al. [109], [110]. First, considering the experimental setup that employs one reference view for rendering, it can be observed in Figure 7.5 that the proposed joint bit-allocation framework consistently outperforms the pre-defined depth bit-rate coding scheme. For example, when inspecting Figure 7.5(a) and Figure 7.5(b), it can be seen that the joint bit-allocation framework yields a quality improvement of 0.8 dB and 1.0 dB at a bit rate 75 kbit per frame, respectively. Additionally, employing the sub-optimal search does not sacrifice the rendering performance compared to full search. Next, let us consider the second experimental setup that uses two reference views for rendering (see Figure 7.6). It can be first noted that the proposed bit-allocation framework also consistently outperforms the pre-defined depth bit-rate coding scheme. Specifically, a rendering-quality improvement of up to 0.9 dB and 0.4 dB is obtained for the sequences “Breakdancers” and “Ballet”, respectively. Note that the depth of the “Ballet” sequence is encoded at 20% of the texture bit rate because a ratio of 10% is not sufficient and even provides annoying results in terms of noise. Again, as previously observed, a fast hierarchical search can be employed without loss of rendering quality. Thus, the sub-optimal hierarchical search provides a fast and accurate estimation of the optimal R-D point of operation.

Additionally, as expected, the rendering quality does not only depend on the sequence characteristics, but also on the rendering structure. For example, a rendering quality of 31.2 dB and 32.5 dB can be obtained at a total bit rate of 150 kbit per frame for the depth and texture images when using one and two reference views, respectively. This result simply highlights that the rendering quality, and thus, the bit-rate distribution is not only influenced by the texture and depth characteristics of the sequence, but also by the number of reference views employed for rendering. Finally, it can be noted that the R-D curve, which is obtained by optimizing the quantization parameters, presents a smooth logarithmically increasing rendering quality. In contrast, not optimizing the quantization parameters yields an R-D curve with non-smooth and even erratic rendering quality.

(a)

(b)

Figure 7.5 (a) and (b) Obtained rendering quality for the sequences “Breakdancers” and “Ballet”, respectively, when performing joint bit allocation using one reference view.

(a)

(b)

Figure 7.6 (a) and (b) Obtained rendering quality for the sequences “Breakdancers” and “Ballet”, respectively, when performing joint bit allocation using two references views.

Finally, Table 7.1 summarizes the measured rendering distortions for the “Breakdancers” and “Ballet” multi-view sequences and the two rendering structures depicted in Figure 7.4. As expected, it can be noted that the ratio between the depth and texture bit rate depends not only on the multi-view sequence, but also on the number of reference views employed for rendering. Specifically, let us select four R-D points corresponding to the maximal rendering quality in the Tables denoted (a) (b) (c) and (d) (see Table 7.1). These four points (underlined in the table) are selected such that the sum of the texture and depth bit rates is less or equal to 100 kbit/frame, i.e., \(R_{max}\leq 100\). For the “Breakdancers” sequence, it can be seen that the depth bit rate corresponds to 40% and 29% of the total bit rate when using one and two reference views, respectively. Next, for the “Ballet” sequence, a bit-rate ratio of 50% and 38% is measured, when using one and two reference views, respectively. Therefore, significant variations in bit-rate distribution are observed for the two multi-view sequences. The obtained bit-rate ratios can be explained by examining the properties of the multi-view sequences. Specifically, the “Ballet” sequence shows richer 3D content when compared to the “Breakdancers” sequence. As a result, rendering high-quality virtual images of the “Ballet” sequence requires a higher depth bit rate when compared to the “Ballet” sequence.

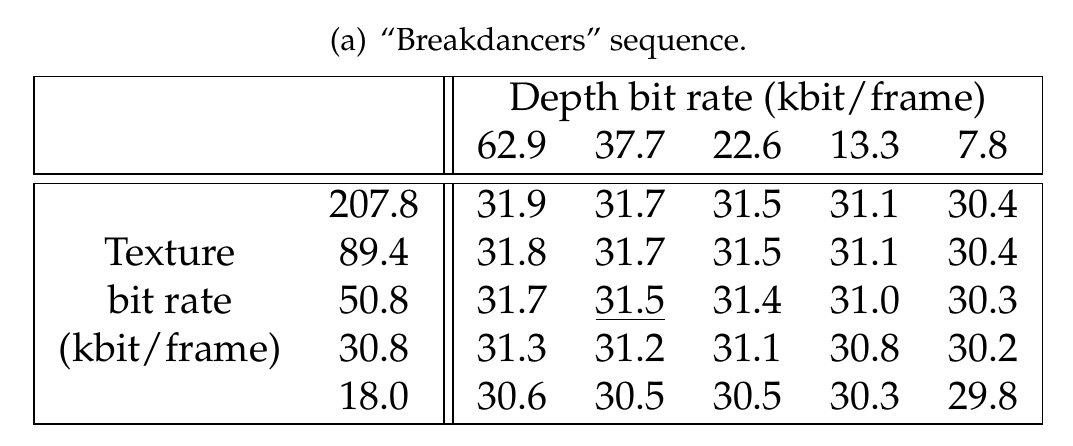
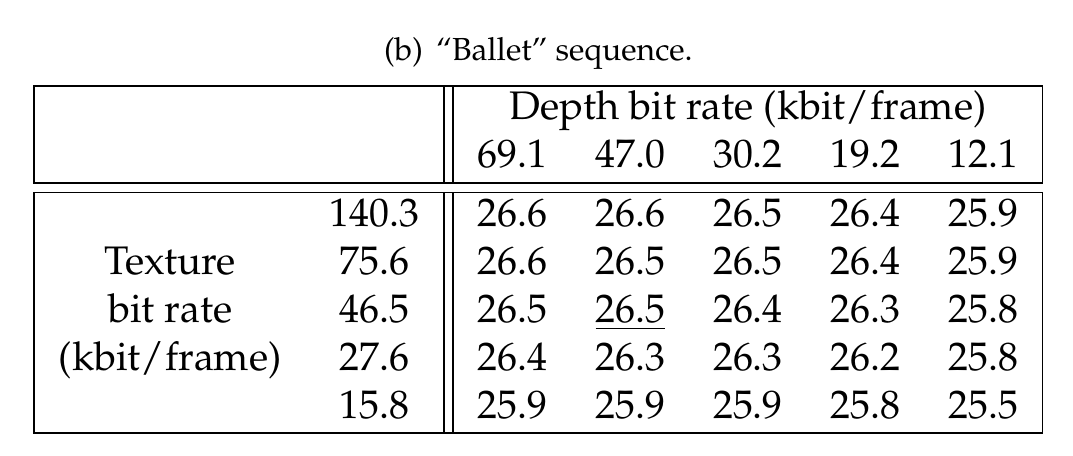
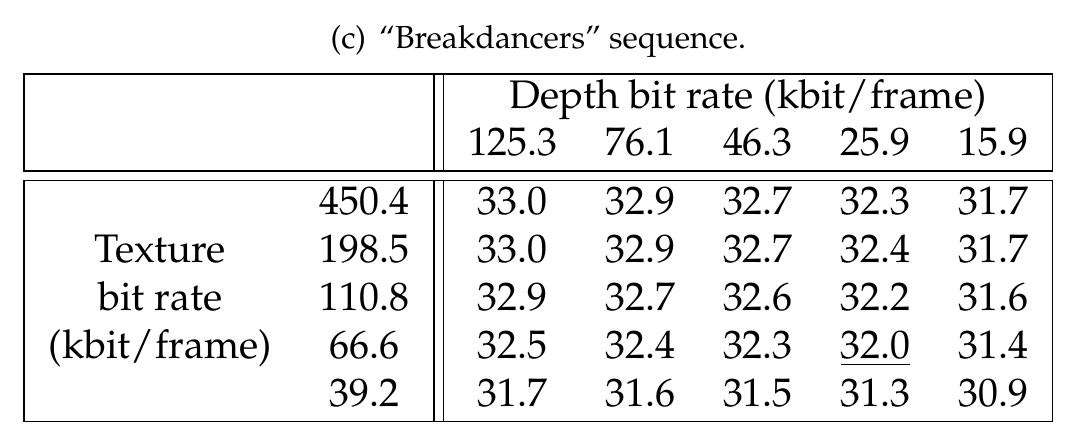
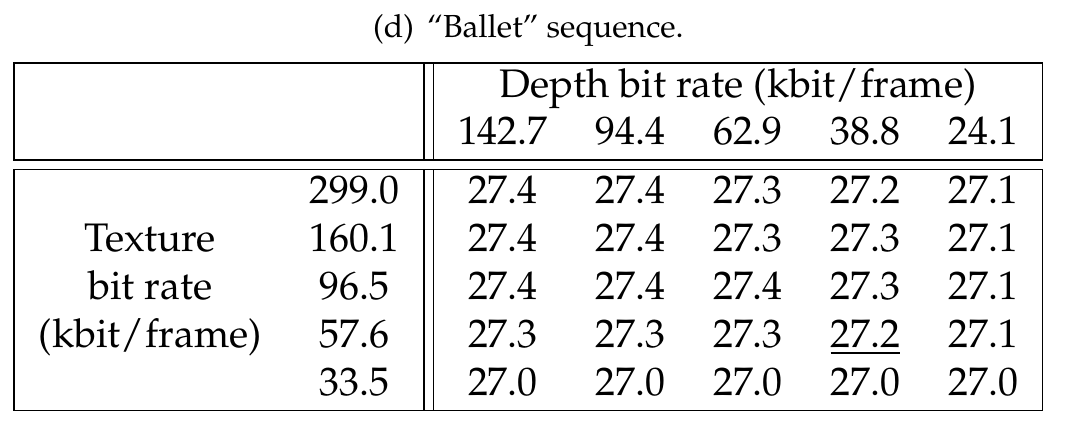
Table 7.1 (a) and (b) show the rendering quality (PSNR in dB) using one reference view. (c) and (d) show the rendering quality (PSNR in dB) using two reference views. The underlined points corresponds to the maximal rendering quality for \(R_{max}\leq 100~kbit/frame\).

Conclusions

In this chapter, we have presented a joint depth-texture bit-allocation algorithm for the compression of multi-view images. To perform a joint bit-allocation optimization, we have proposed to combine both the depth and texture R-D curves into a single unified R-D surface. We have empirically verified that the R-D surface presents smooth monotonic properties so that fast optimization algorithms can be employed. A hierarchical search for estimating the optimal quantization parameters, which is similar to the Tree-Step Search for motion estimation, was implemented. Experimental results have revealed that the performance is comparable to a full-search parameter optimization. Because the algorithm features low computational complexity, the described joint bit-allocation optimization technique can be readily integrated into the N-depth/N-texture multi-view encoder, which is currently investigated within the FTV framework of MPEG.

The original problem statement mentioned at the beginning of this chapter formulated the R-D optimization as a function of the coding of texture and depth signals and the applied rendering. In the experiments, we have employed a specific rendering algorithm to come to feasible results. However, the total optimization should encompass an optimization of the rendering algorithm as well. This was beyond the scope of this thesis.

The concept as posed in this chapter does not only apply to 3D-TV transmission, but also to other cases where geometry and depth is encoded, such as in computer graphics. In such a case, the rendering function would have a different behavior and may be different specifications, but it would play an equally important role in the problem statement and optimization. Similarly, the concept can also be applied to different coding algorithms involving the compression of geometry and texture signals.

References